Chromie Squiggles: Segments Decoded

By: Yamamoto

Note: This is part 1 of a multi-part series on the Chromie Squiggle traits. I will be releasing a new essay roughly every day or two for the next two weeks.

Summary: This will be a deep dive into the segments trait. We'll explore what a segment is, and some of the hidden rarities that I believe were previously unknown.

TLDR:
-Segments are always one segment shorter than the trait data states. Sometimes two segments shorter.
-The possible range for segments is 10-19, not the currently stated 12-20.
-Squiggles with 10 segments are the rarest (1 in 256 chance)
-Squiggles with 20 segments don't actually exist; they are actually 18-segment Squiggles.

What is a Segment?

Squiggles are made up of hundreds or thousands of circles, also known as steps. These circles are grouped into segments. The current trait data says Squiggles can have anywhere from 12 through 20 segments.

Here you can visualize the segments in a squiggle.

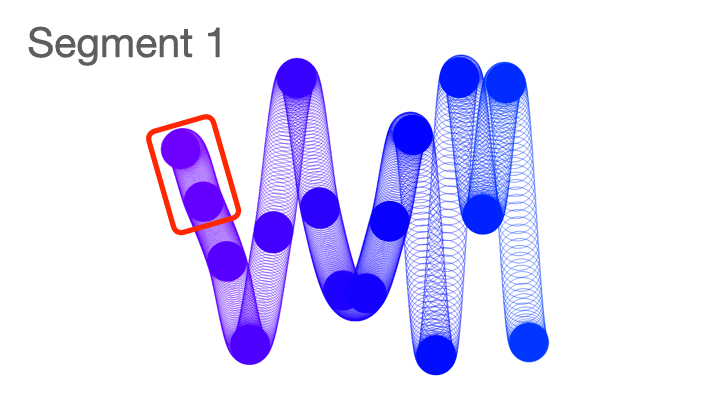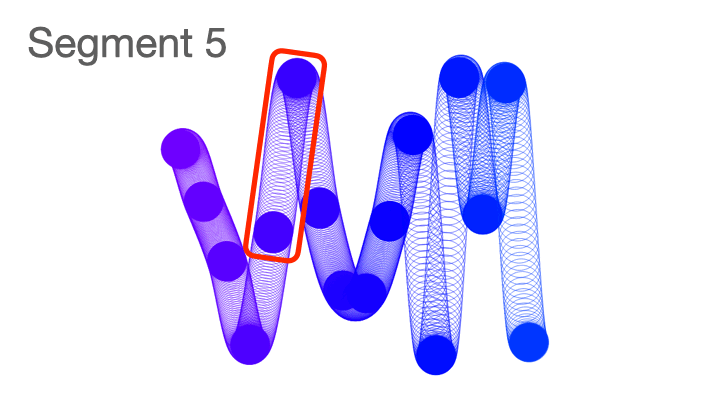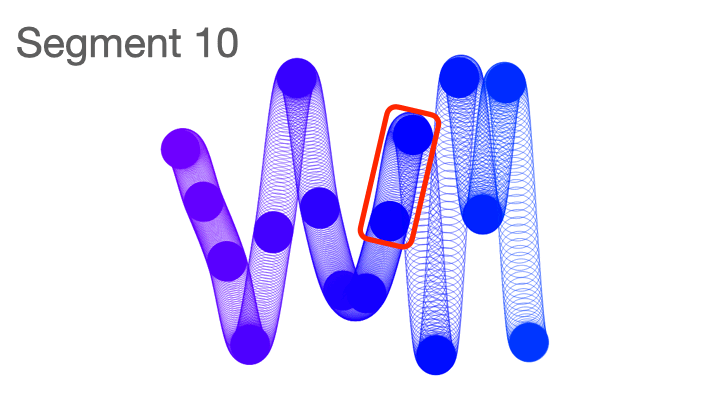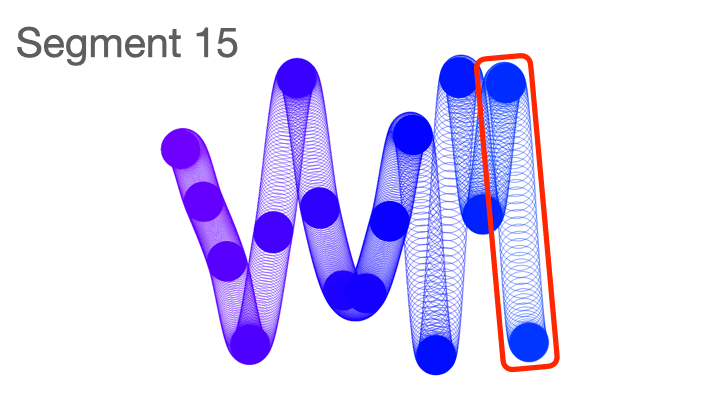
The more segments a squiggle has, the longer it will appear.

Here's another way to view it where I froze the code after each segment was created.

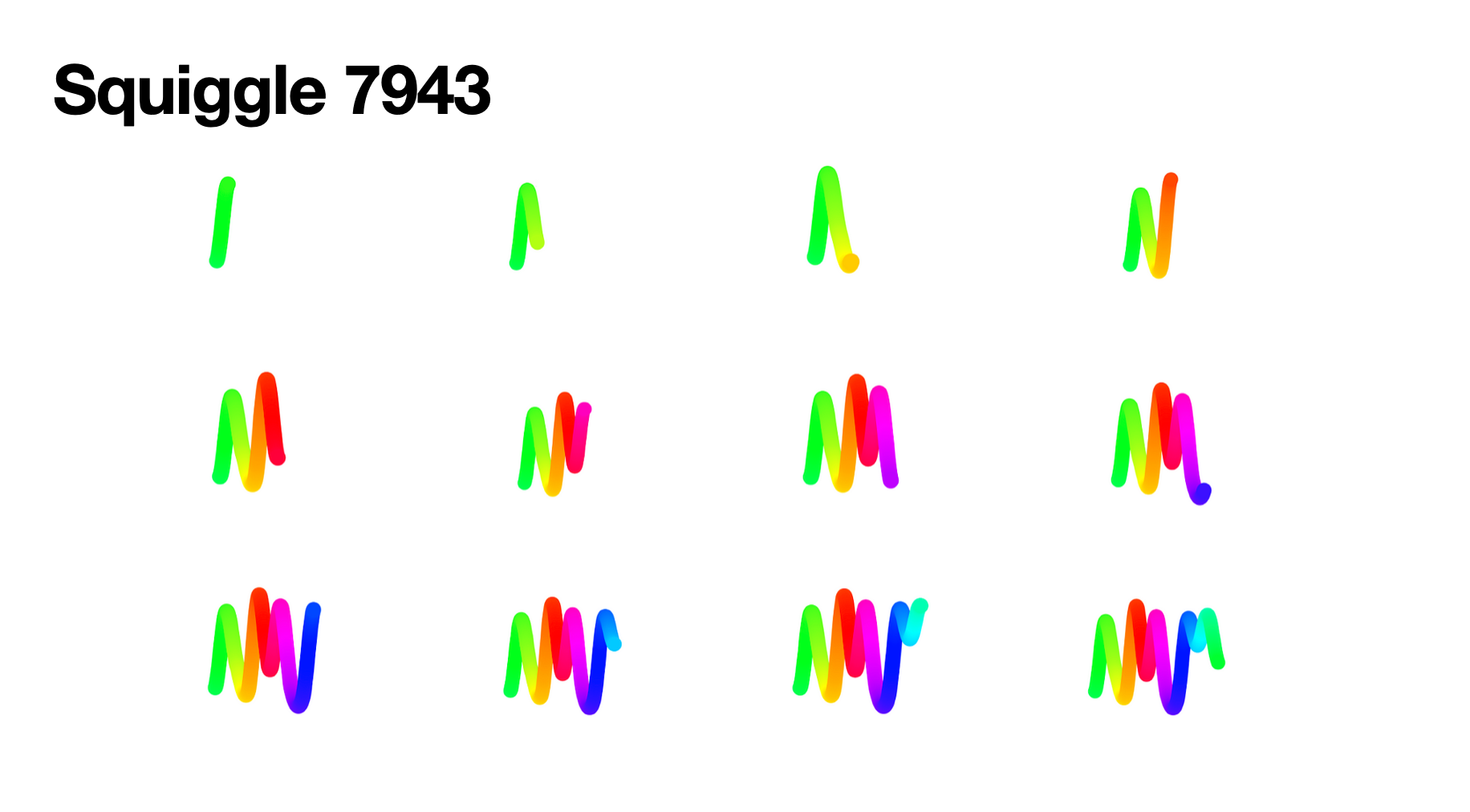
It's easiest to visualize segments is using slinkies and pipes, as they tend to have clearly defined starting and end points. Sometimes it's hard to spot where one segment ends, and the next begins, because they go in the same direction, or an entire segment occurs at the curve point of the squiggle.

Why is the Segments trait innacurate?

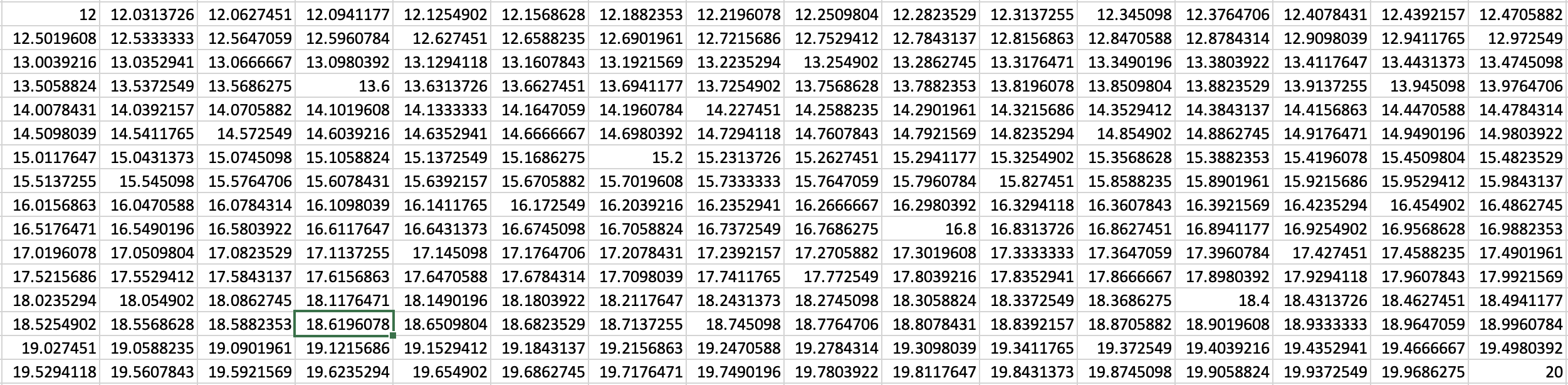
In the official trait data, segments are listed 12-20. When the code runs, there are actually 256 decimal-precise segment values.

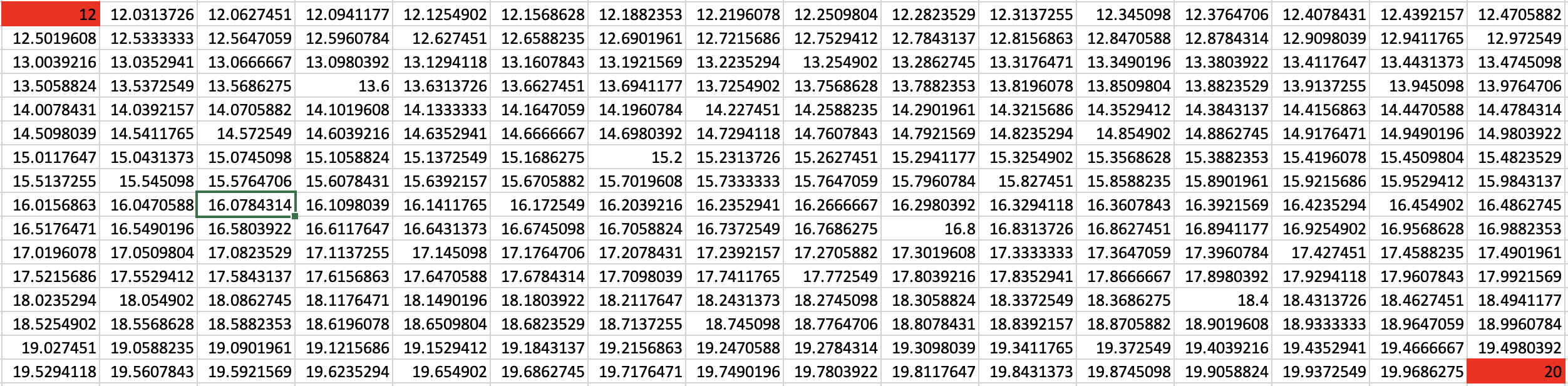
Here's all 256 possible segment values.

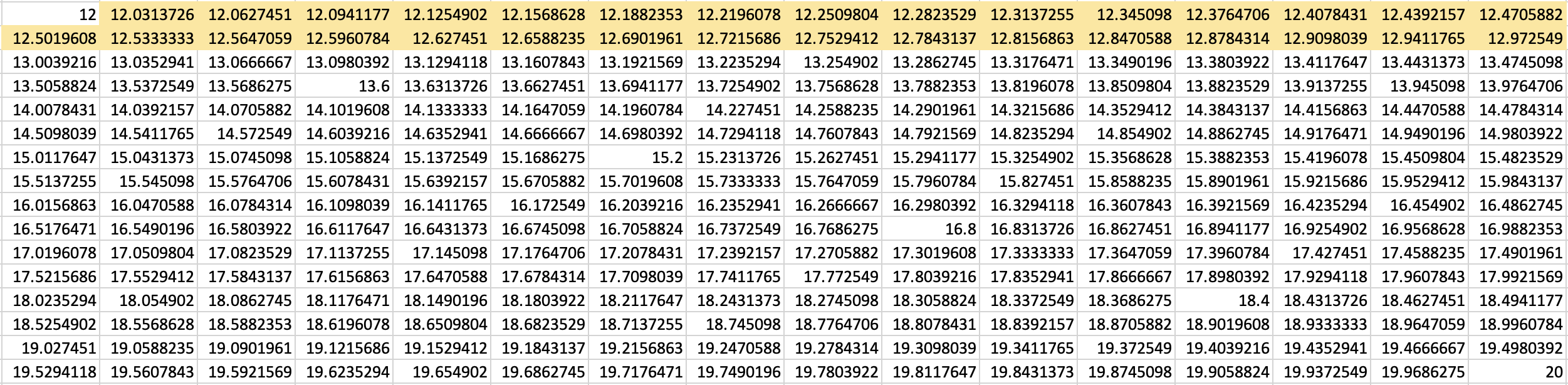
In the official trait data, these numbers were rounded down. For example, the highlighted twelve-decimal values below were all rounded to 12.

So how does this make segments one short? Let's look at the code.

Here's the code that creates the segments.

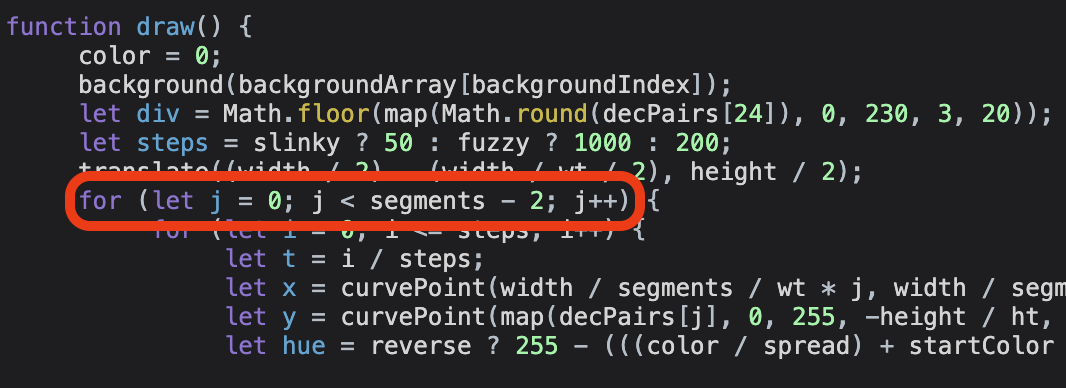
The code keeps creating segments until the number of segments it has generated is no longer less than segments minus two. So for a squiggle with a 12.2509804 segment variable, the code creates segments 0 through 10, which is 11 total when accounting for it starting at 0.

Let's break it down into smaller pieces so this makes more sense.

Using segment 12.2509804 as an example. The code actually looks at segments - 2, so 10.2509804.

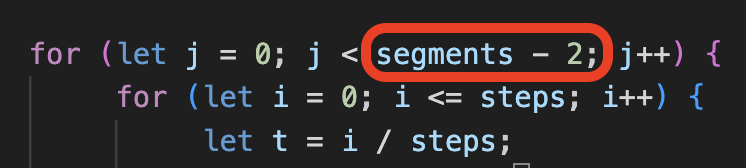
The code keeps creating segments until the number of segments it has generated is no longer less than 10.2509804.

So for this example, it creates segment 0, 1, 2, 3, 4, 5, 7, 8, 9, 10, and it stops at 10, because the next segment would be 11, and 11 is not less than 10.2509804.

0 through 10 is 11 total segments.

If the code had instead been written, segments minus 1, it would generate the correct 12 segments, and the trait data we've been using would have been correct.

What about Squiggles with two less segments?

If you look at the image of all the possible segment values, you'll notice two of the numbers are whole numbers. 12 and 20.

These two segments will actually be two short. If we run through the example above with the whole number 12, instead of 12.2509804, the code will keep creating segments until the next segment greater than 10 (segments - 2).

The code creates segment 0, 1, 2, 3, 4, 5, 7, 8, 9, and it stops at 9, because the next segment would be 10, and 10 is not less than 10.

0 through 9, so 10 total segments. Here's one I generated segment by segment to illustrate this.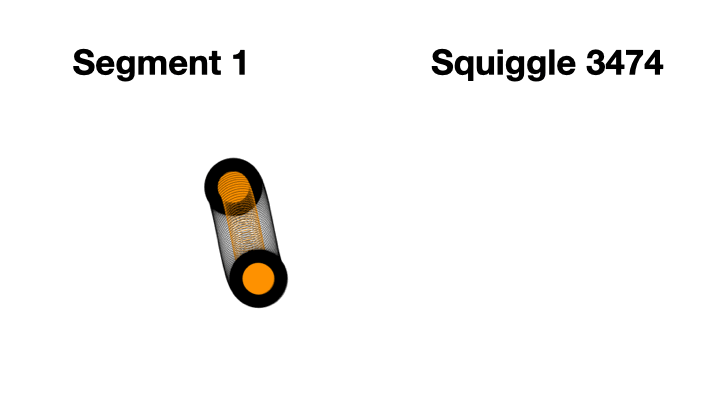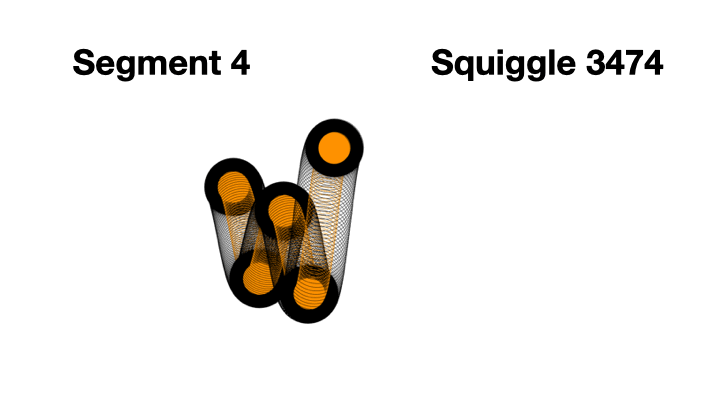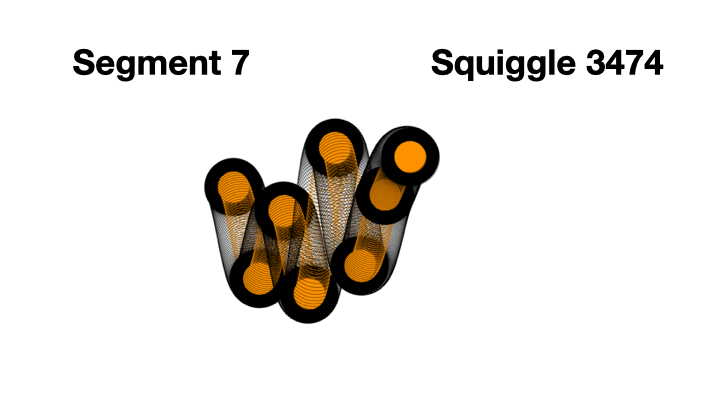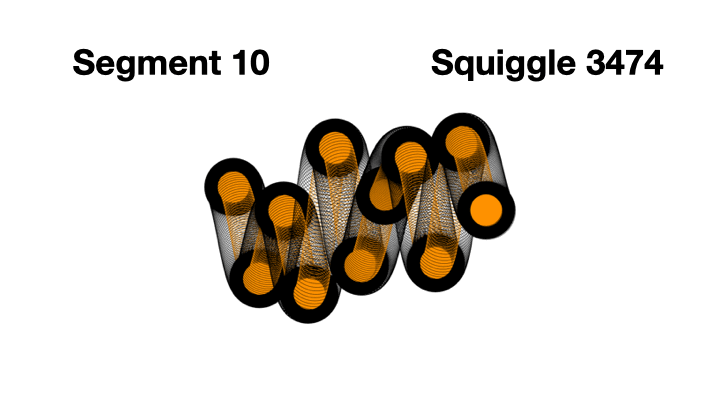

Run the Code Yourself

Below is a code snippet where I have simplified the code to just run the segment loop exactly as the algorithm does. It doesn't create a squiggle, it just tells us when a segment was created.

I defaulted 12.2509804 as segments from our example, but you can change that value to be any number you want and experiment to see how many segments the code actually generates.

You'll need to scroll in the terminal below to see all the iterations

Summary

In conclusion, the number of segments is always one short and sometimes two short. When Art Blocks originally documented the segments, they likely just took the segment variable and rounded down for simplicity.

This revelation also introduces some new rarities that we were previously unaware of. There is a 1 in 256 chance of minting the shortest possible squiggle, a 10 segment squiggle.

It also means that 20 segment Squiggles, in fact have 18 segments. The same number as any 19 segment squiggle.

With generative art, there are times when traits describe something visually, but not algorithmically accurate. There's also situations where traits can focus on the algorithm, but not visuals. In this situation, this trait neither represents the squiggle visually, nor what the code did algorithmically, making segments particularly challenging to navigate.

It was wise for the Art Blocks team to round the segments, since the algorithm will only ever process a whole segment, not a fraction of one. Unfortunately, the rounding system used obfiscates the true nature of the squiggle and provides broadly inaccurate data. It even leads to consumers paying premiums for 20 segment Squiggles, that are in fact 18's.

In a world where truth is increasingly elusive, we moved to the blockchain to ensure transparancy and data integrity. Not to be too harsh, but if we expect Squiggles to one day be in the Louvre, and be collected by the most important institutions and collectors around the world, we can't have major oversights on the most basic of traits.

If the Art Block's team is interested in correcting this data, the simplest way is to take the decimal precise variable, round it up, and subtract 2. This would account for both the 1 and 2 segment discrepancy, and provide a whole number that accurately reflects the visual and algorithmic nature of the Squiggle.

If you want to see the segment data for every squiggle, you can check out this Squiggle Drive Sheet with every Squiggle's data documented.

Lastly, it appears that segment data was used to calculate other downstream traits, such as end color, which I will explore in future essays along with some of the anomolies discovered in the steps and color spread traits.

I hope you enjoyed this, I welcome feedback. @Yamamoto